Puzzle from Reddit (link)
04/19/2015My friend linked me a programming puzzle on Reddit and I found it interesting. I didn't get anywhere thinking about it, but I brought it up with my friends and we came up with a neat solution. This post outlines our approach to solving the puzzle (solution below, pardon my artwork as always).
Problem description
As a brief problem description, you are given N input statements giving us the probabilities of various combined events. For instance, in the default example above, the input/output should read:
or, the event "Not A and B" happens with probability 1%. Given many probability assignments like this, the challenge is to find the probability of a target event; in the example above, this is P(A & !B).
Renaming variables for convience in linear algebra
The input statements are not conducive to linear arithmetic manipulation in their undoctored form. For instance, if we are given
we can't combine those equations to get P(A & B), P(A || B), P(A & !B), or really any meaningful combination of the two events; in order to do so we need some quantitative metric of how related A and B are. Notably, however, if we knew that A and B were mutually exclusive, then we can set up linear systems where the probability of one event or another is simply the sum of the two individual probabilities. And that's the first trick - rephrasing the inputs as combinations of mutually exclusive events.
In a universe of N boolean events, there are 2N different, mutually exclusive, outcomes. Specifically, let's label the original events X0, X1, ..., XN-1, and label the entire universe outcomes Y0, Y1, ..., Y2N-1. Let's assume that Y0 corresponds to the specific outcome of
and Y1 corresponds to
and Y2 corresponds to
etc, "incrementing" from "not Xi" to "Xi" like counting in binary.
If we rephrase the problem inputs in this grammar, using Y instead of X, we now get the benefit of knowing that each of our "events" are mutually exclusive; only one element of the Y0 ... Y2N-1 sequence can be true. Because of this, we can add and subtract probabilities and use linear algebraic reasoning. To make this transition, define Y'i as P(Yi) for all i in [0, 2N-1].
Solving the example
Bringing this back to a concrete example, let's start with the example given in the dashed brown box, except let's rename A to be X0 and B to be X1 to be consistent with our naming conventions. We then have
This can be rephrased in the new "Y"-grammar defined above as follows:
Note that X1 actually corresponds the union of the two events, X1 & !X0 with X1 & X0, which is why X1 corresponds to Y1 || Y3. Anyway - we can again rephrase in the new " Y' "-grammar:
As you may have realized, there's an additional equality which goes unsaid - the sum all of everything in the Yi sequence adds up to 1. Recall that the universe is exactly partitioned into the Yi sequence. So, our final linear system is
which we can easily solve with Gaussian row reduction.
Incomplete information
If we take a step back, we solved the example problem by finding the probability of every single true/false assignment to each of the input events. If they've given us enough information, then this is a fine approach. But what if the question was just
In this case, we don't have enough information to solve for all of {Y'0, Y'1, Y'2, Y'3}, but we can still evaluate P(X0), which is Y'2 + Y'3. Rewritten in the " Y' "-grammar,
Re-written again as a matrix, M,

This is the second trick of this problem. How can we solve one particular linear combination of variables without solving for all of the variables? The naive Gaussian elimination hinges on being able to solve for all variables and is therefore not a valid solution. One solution is to find some combination of the input expressions which gives you the specific linear combination you're looking for. In the example above, note that
So the problem has changed from solving for Yi to solving for the coefficients of the input equations which you can combine to get the desired linear combination!
To set up the new linear system (which solves for the coefficients of the input equations, not for Yi) we can take the transpose of the unaugmented M matrix, and augment it with the coefficients of the desired linear combination. Neat, right? We are now solving for the coefficients we can use to linearly combine the input equations to get our desired probability. Here is the resultant augmented matrix. The left-side is the transpose of M and the right side is coefficients of Yi representing our desired probability, which is Y2 + Y3.

which, using Gaussian row reduction, we can simplify to

The right-side coefficients here can be used to linearly combine our inputs with our inputs, M to get our desired answer. In matrix form, this is
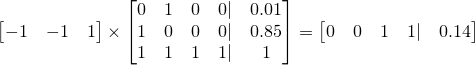
to give our final answer of 0.14 for this problem. And that's all there is to it!
